В прямоугольном треугольнике сумма квадратов длин катетов равна квадрату длины гипотенузы.
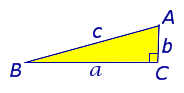
c2 = a2 + b2
Через произвольные точки A1, A2, … An–1, An, лежащие на стороне AO угла AOB, проведены параллельные прямые, пересекающие сторону угла OB в точках B1, B2, … Bn–1, Bn, соответственно. Тогда справедливы равенства ОА1 / ОВ1 = А1А2 / В1В2 = А2А3 / В2В3 = … = Аn-1An / Bn-1Bn
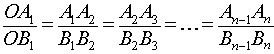
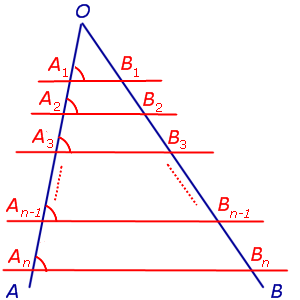
Квадрат длины стороны треугольника равен сумме квадратов длин других сторон минус удвоенное произведение длин этих сторон на косинус угла между ними.
a2 = b 2 + c 2 – 2bc cos A
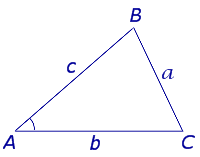
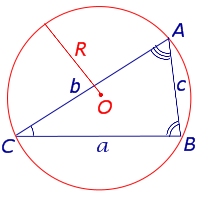
Для любого треугольника справедливы равенства: a \ sinA = b \ sinB = c \ sinC = 2R
![]()
R — радиус описанной около треугольника окружности.
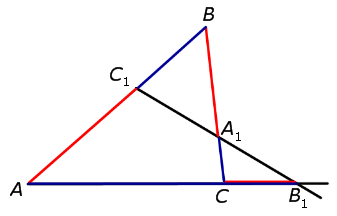
Если на сторонах AB и BC треугольника ABC взяты соответственно точки C1 и A1, а точка B1 взята на продолжении стороны AC за точку C, то точки C1, A1 и B1 лежат на одной прямой тогда и только тогда, когда выполнено равенство
АС1 \ С1В * ВА1 \ А1С * СВ1 \ В1С = 1
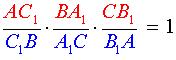
Авторизуйтесь, чтобы оставить комментарий.