Азы комбинаторики

Что такое комбинаторика и зачем оно нам надо на ЕГЭ по информатике?   

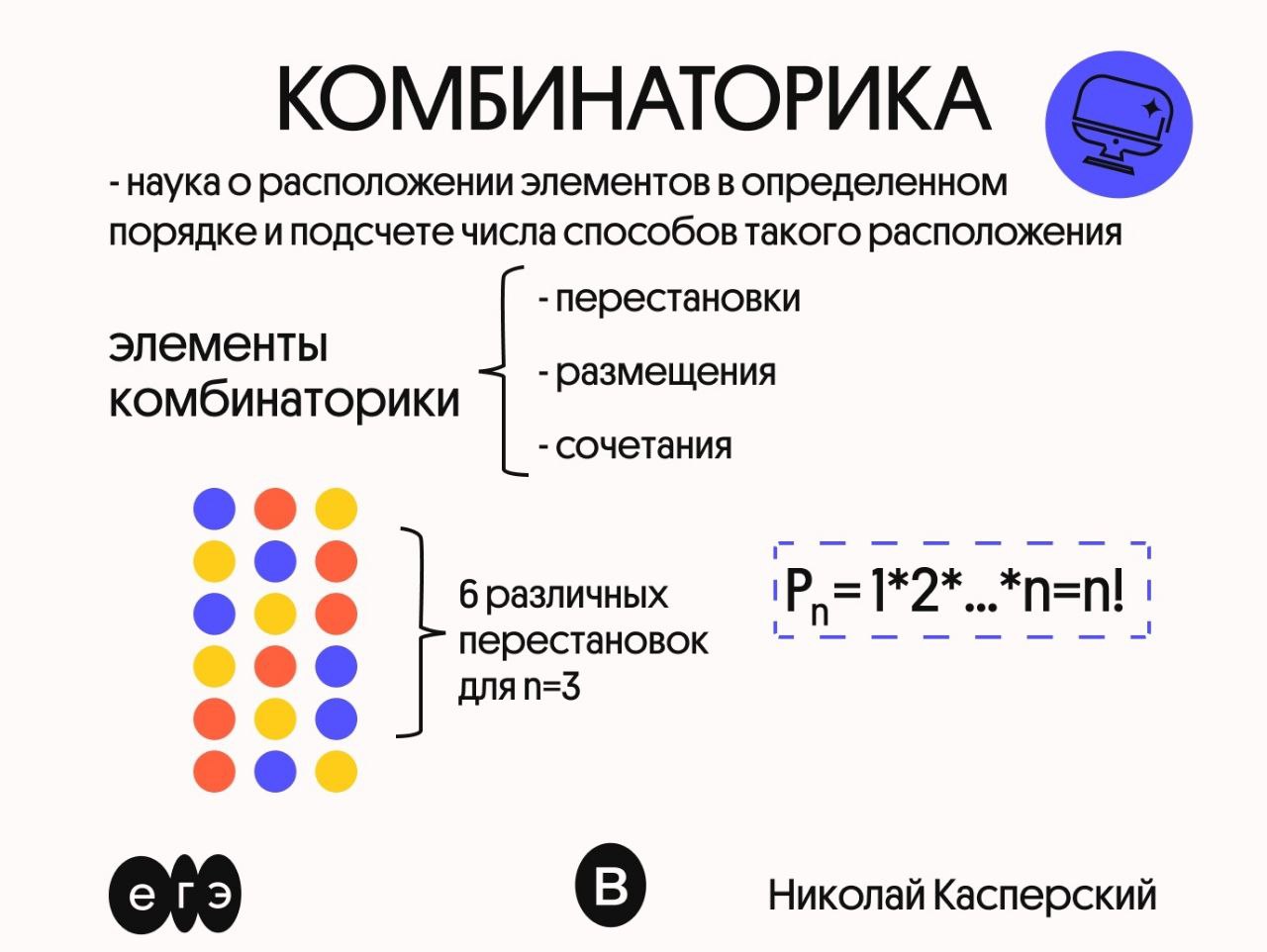
  Рассмотрим элементы комбинаторики: бывают перестановки, размещения и сочетания. 

  ◾ПЕРЕСТАНОВКИ 

  Перестановками называются такие выборки элементов, которые отличаются только порядком расположения элементов.    

   Представь, что у тебя есть 10 книжек и тебе необходимо их расставить на полке в каком-то порядке, так сколько способов это сделать у тебя есть? 

   Формула подсчета перестановок: 

  📍Pn = n·(n−1)·(n−2)…3·2·1 = n!, где n- количество элементов данного множества. 

  ! — это факториал числа — произведение натуральных чисел от 1 до самого числа (включая данное число. 

  То есть, решением поставленной задачей будет: P(10) = 10·(10−1)·(10−2)…3·2··1 = 3628800

◾РАЗМЕЩЕНИЯ 

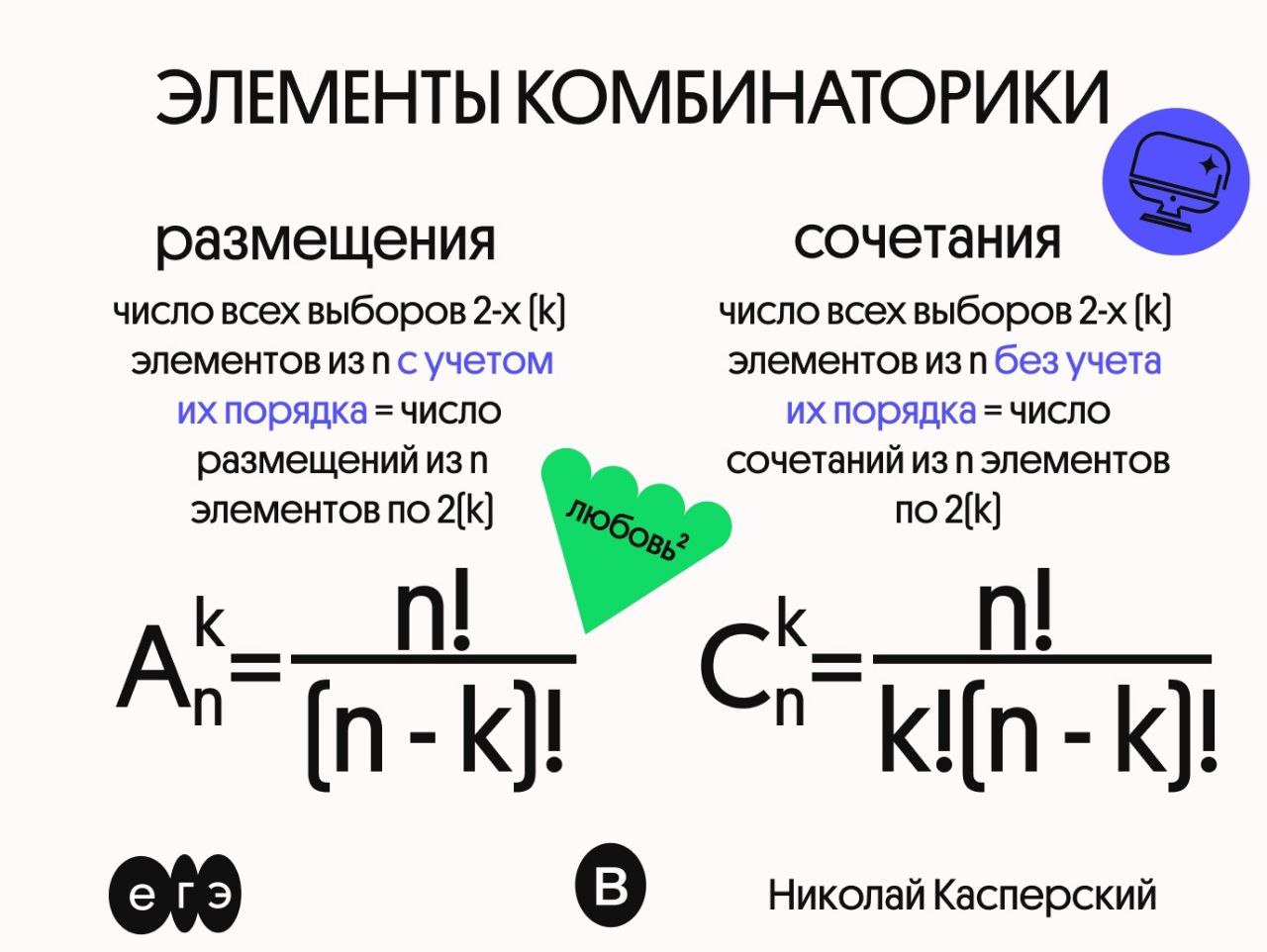
  Размещениями из n элементов по m (мест) называются такие выборки, которые имея по m элементов, выбранных из числа данных n элементов, отличаются одна от другой либо составом элементов, либо порядком их расположения. 

  Например, тебе уже надо не все 10 книжек расставить по порядку, а только 5 из них,так вот сколько будет способов это сделать? 

   Число размещений из n по m обозначается A(n;m) и определяется по формуле 

  📍A(n;m) = n·(n − 1)·(n − 2)·…·(n − m + 1) = n!/(n − m)! 

  Так вот количество способов подсчитать такое расположение пяти книжек из 10 на полке и будет число размещений из 10 по 5. То есть: A(10;5) = 10!/(10 − 5)! =10!/5!=30240 

  ◾СОЧЕТАНИЯ 

  Неупорядоченные выборки называются сочетаниями из n элементов по m и обозначаются С(n;m) 

  Ключевое слово здесь неупорядоченные, то есть нам не важно, какая книжка будет стоять на первом месте, а какая на втором, мы хотим посчитать любые варианты расстановки. Можно интерпретировать как: у нас все также есть 10 книжек, пять из которых нужно расставить в любом порядке, сколько существует возможных вариантов? 

  📍Число сочетаний определяется по формуле С(n;m) = n!/((n − m)!*m!)    

  То есть в нашей задаче получится: С(10;5) = 10!/((10 − 5)!*5!)= 252 

ВАЖНО: далеко не всегда в ЕГЭ применяются формулы комбинаторики (иногда задачу проще решить перебором), но в любом случае знать основы необходимо.