Свойства сторон и углов треугольника

Сумма углов треугольника равна 180°:

α + β + γ = 180°

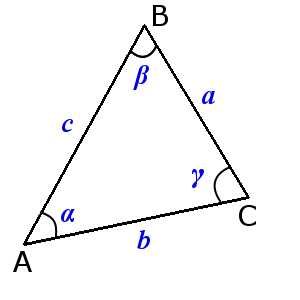
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:

если α > β, тогда a > b

если α = β, тогда a = b

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:

a + b > c

b + c > a

c + a > b

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов.

Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

a2 = b2 + c2 — 2bc·cos α

b2 = a2 + c2 — 2ac·cos β

c2 = a2 + b2 — 2ab·cos γ

Теорема о проекциях

Для остроугольного треугольника:

a = b cos γ + c cos β

b = a cos γ + c cos α

c = a cos β + b cos α

Формулы для вычисления длин сторон треугольника

Формулы сторон через медианы

a=2/3√2(mb2 + mc2) — ma2

b=2/3√2(ma2 + mc2) — mb2

c=2/3√2(ma2 + mb2) — mc2

Биссектрисы треугольника

Определение.

Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.

Свойства биссектрис треугольника:

1. Биссектрисы треугольника пересекаются в одной точке, равноудаленной от трех сторон треугольника, — центре вписанной окружности.
2. Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
   AEAB = ECBC
3. Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
   Угол между lc и lc‘ = 90°
4. Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный.

Формулы биссектрис треугольника

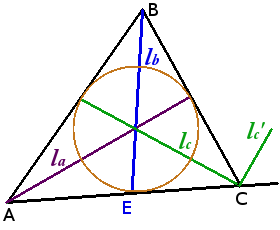
Формулы биссектрис треугольника через стороны:

la = 2√bcp(p — a)/b + c

lb = 2√acp(p — b)/a + c

lc = 2√abp(p — c)/a + b

где p = a + b + c/2  — полупериметр треугольника

Формулы биссектрис треугольника через две стороны и угол:

la = 2bc cosα2b + c

lb = 2ac cosβ2a + c

lc = 2ab cosγ2a + b