Степени с разными основаниями

✅ Степенью называется выражение вида: a^n, где:

a — основание степени;

n — показатель степени.

Возвести число в натуральную степень n — значит умножить число само на себя n раз:

a^n = a ⋅ a ⋅ a ⋅ … a, и так n раз.

💁🏼‍♀ Для натуральной степени понять, что происходит максимально просто. Но есть два нюанса: основание степени может принимать положительные или неотрицательные значения.

❓ Каким оно может быть?

В степенях с натуральным показателем основание может быть любым числом. И правда, мы ведь можем умножать друг на друга любые числа, будь они положительные, отрицательные, или даже 0.

❓ Давайте подумаем, какие знаки («+» или «−») будут иметь степени положительных и отрицательных чисел?

Все довольно просто:

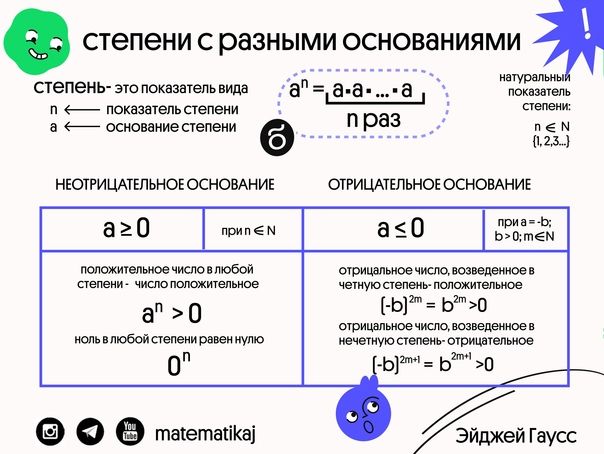
✅ Отрицательное число, возведенное в четную степень – число положительное.

(−2)^4 = 16

Отрицательное число, возведенное в нечетную степень – число отрицательное.

(−2)^5 = −32

Положительное число в любой степени – число положительное.

2^4 = 16, 2^5 = 32

Ноль в любой степени равен нулю.

0^4 = 0, 0^5 = 0