Производная показывает насколько быстро что-то происходит. Насколько быстро идет человек, растет стресс перед экзаменами или увеличивается количество баллов для поступления. Если быть более точным с точки зрения математики, производная — это математическая функция, которая показывает скорость какого-то процесса.
👉🏻 Если мы посмотрим на эту самую функцию производной, то увидим, что есть особые точки, в которых процесс меняется — сначала возрастает, а потом начинает убывать, или наоборот.
🔸 Например, ты беспокоился о поступлении, но потом вдруг сдал ЕГЭ, и стало все равно — стресс падает. Такие точки называют минимумами и максимумами. Именно они помогают нам в заданиях ЕГЭ на производную.

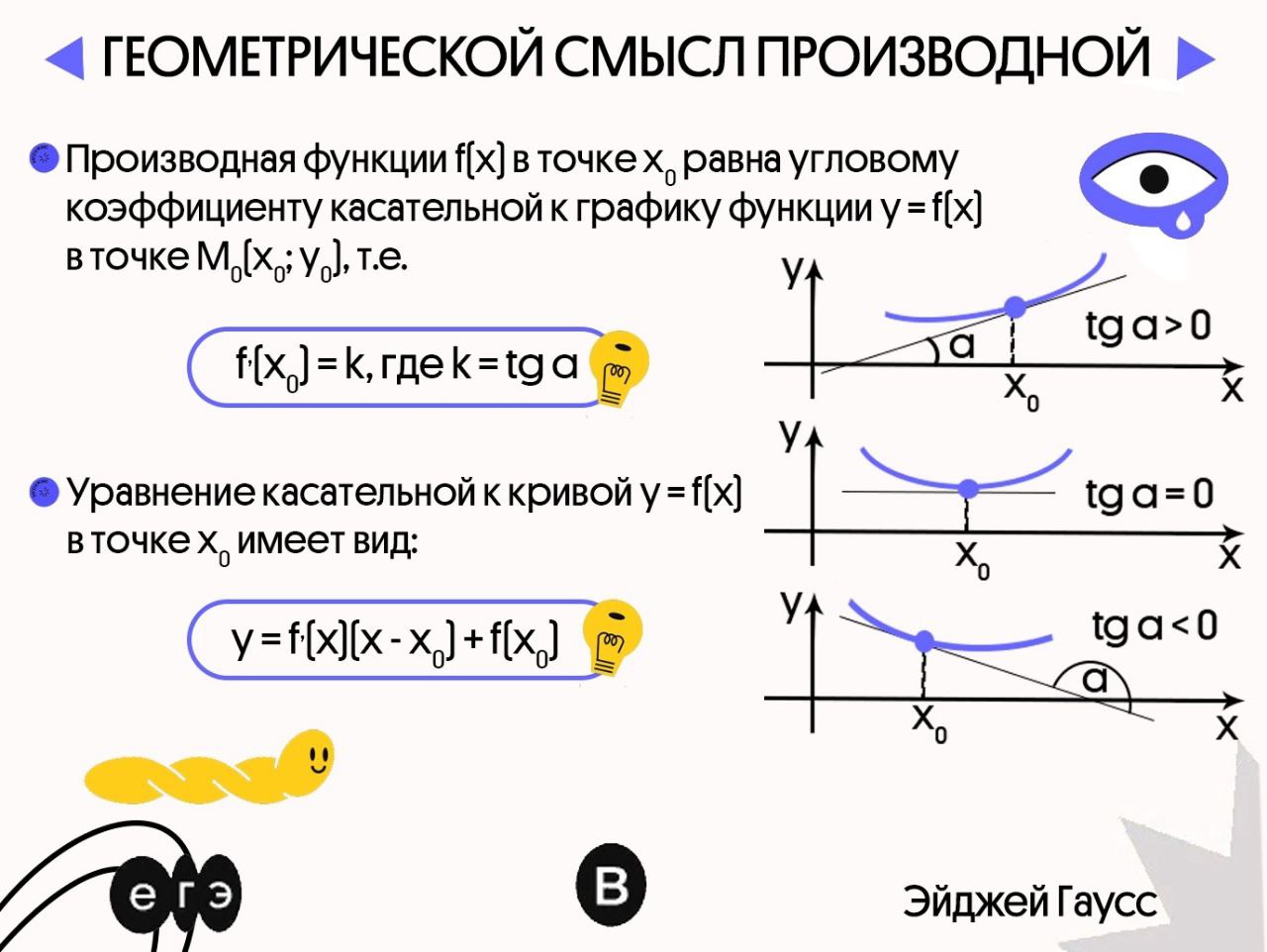
✅ Производная — это показатель скорости изменения функции. Функцию можно нарисовать, и значит производную тоже можно нарисовать на том же самом графике функции. Возьмем на графике функции любую точку и назовем ее x0. И проведем касательную к функции в этой точке. Напомню, что касательная — это такая прямая, которая имеет с функцией в области этой точки только одну точку пересечения x0.
🔹 Эта прямая будет наклонена к оси OX, и у нее есть формула, как и у любой другой прямой — y = kx + b. В этой формуле за угол наклона отвечает коэффициент k. Производная отвечает за возрастание или убывание функции, то есть за наклон функции. И есть три вещи которые отвечают за наклон на этом графике в точке x0: угол наклона, коэффициент k и производная функции.
❗️ И если три разные вещи отвечают за одно и тоже, то скорее всего они равны — так и есть. Производная в точке x0 в точности равна коэффициенту k, касательной проведенной к функции в точке x0, и равна тангенсу угла наклона этой касательной. Это свойство и называют геометрическим смыслом производной. Осталось только понять, что с этим делать и как применять! 🌟
Производная — это специальная функция, которая получается с помощью математической операции бла-бла-бла. Это конечно важно и полезное определение, но появились же производные не так, что кому-то показалось мало обычных функций и он придумал еще одно математическое развлечение.
💁🏻♂️ Было все примерно так — в жизни есть какие-то процессы, например, увеличение известности Инстасамки в интернете. Этот процесс происходит с космической скоростью: вот пару месяцев назад ее никто не знал, и вот ее уже обсуждают даже бабушки у подъездов. А как измерить скорость распространения ее известности — она же сильно увеличивается?
🔸 Раньше для этого нужно было строить график функции популярности смотреть по нему на сколько быстро растете известность в равные промежутки времени и …. Это безумно долго.
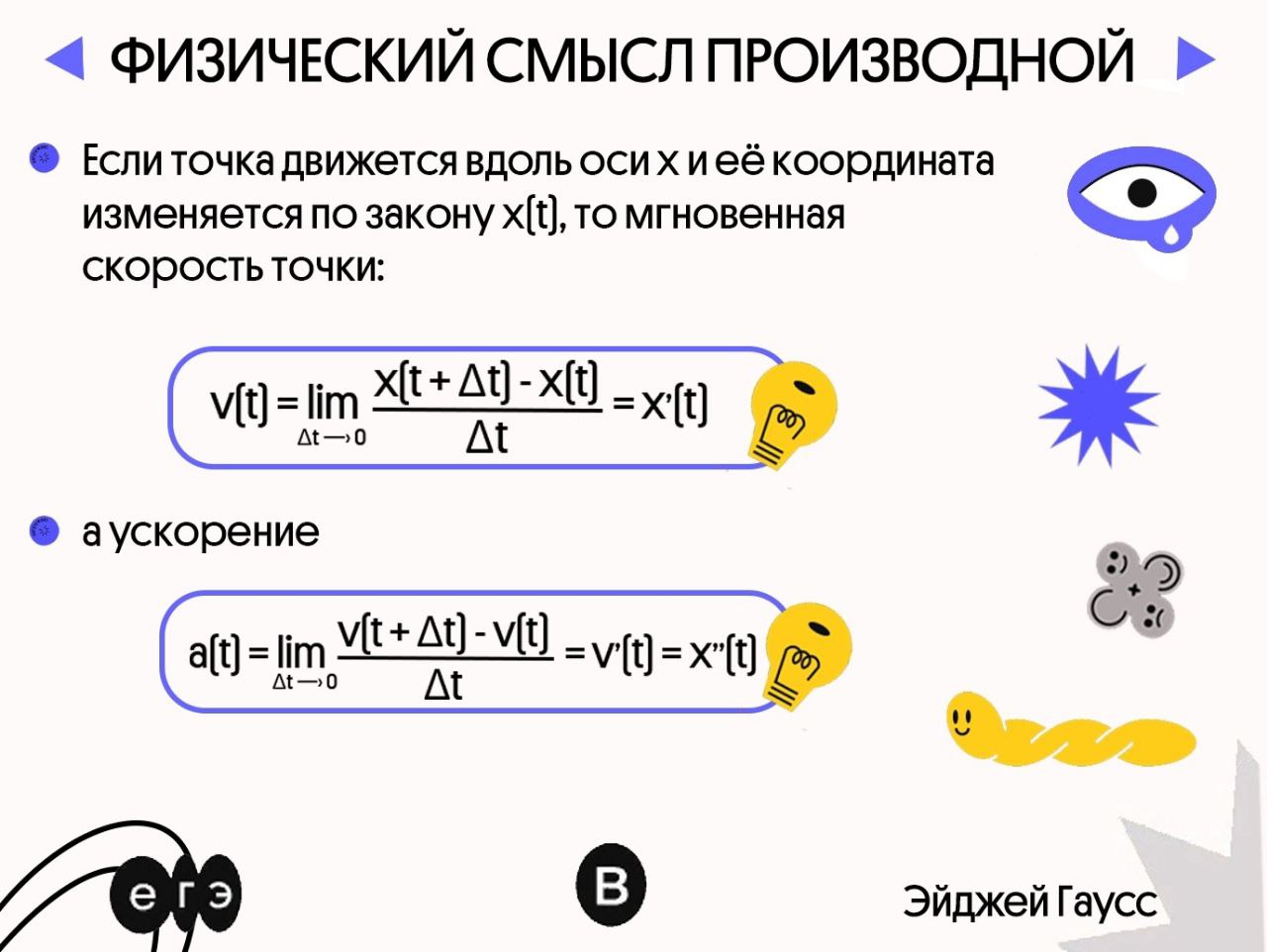
Поэтому чтобы измерять скорость любого процесса и придумал специальную операцию — извлечение производной. А сама производная — это прежде всего скорость какого-то процесса или функции, если речь идет о математике. Отсюда очень естественно выходит физический смысл производной.
✅ Производная от пути — это СКОРОСТЬ изменения координаты от времени или простая скорость. А производная от скорости — это скорость изменения скорости от времени, или самое обычное ускорение. Поэтому чтобы найти скорость нужно извлечь по всем законам математики производную от функции координаты. А чтобы найти ускорение нужно по тем же самым законам извлечь производную от функции скорости.
Авторизуйтесь, чтобы оставить комментарий.