Площади поверхностей фигур

Продолжаем повторять формулы стереометрии, на этот раз площадь поверхности. Площадь поверхности любой пространственной фигуры — это сумма всех площадей её граней. Если простыми словами – это площадь той поверхности, которую можно потрогать у фигуры.

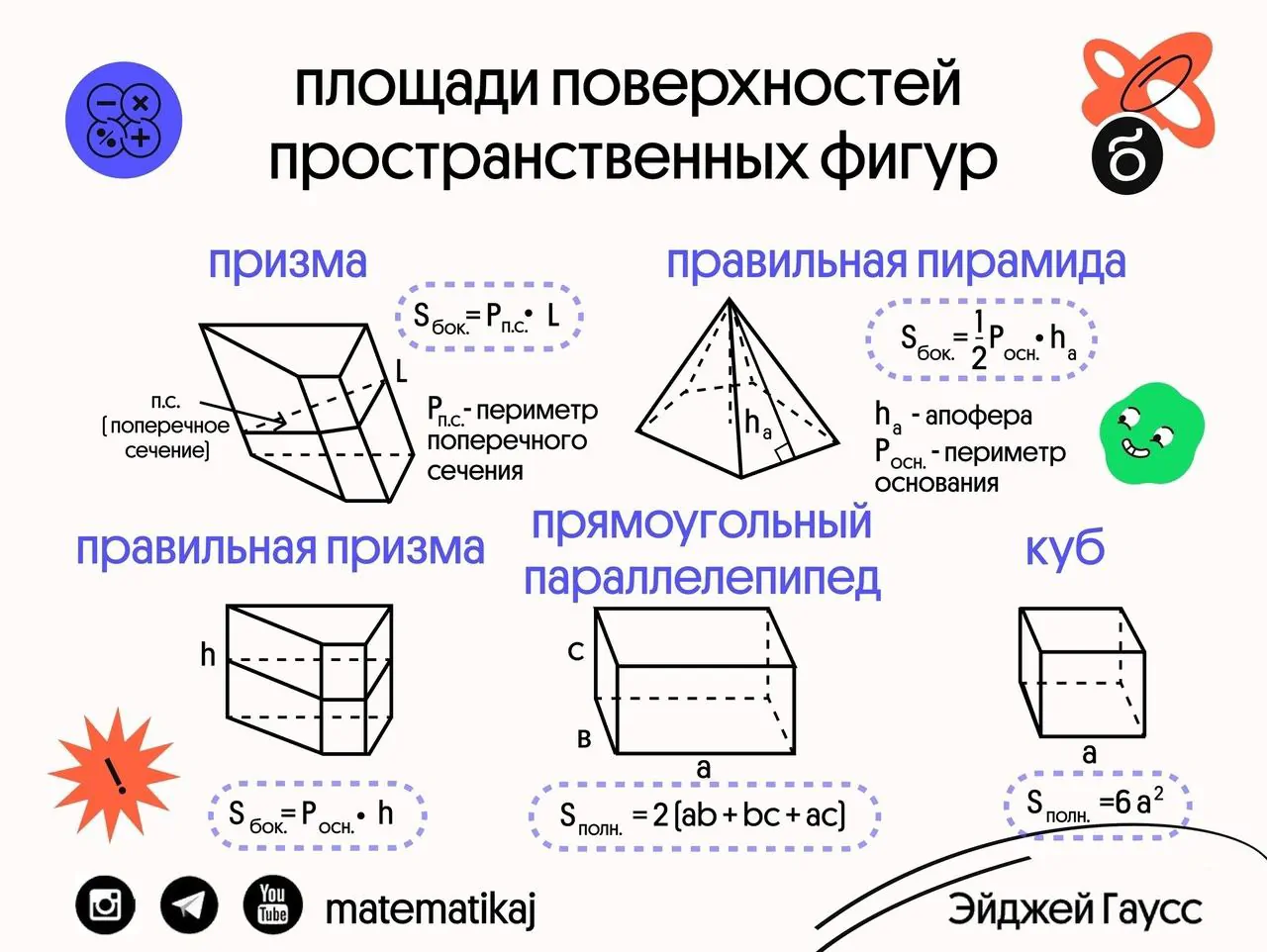
✅ Начнём с куба — у него шесть граней, все они квадраты, поэтому площадь каждой равна a^2, а площадь поверхности куба равна 6 • a^2. У прямоугольного параллелепипеда примерно та же история, у него 6 граней, только на этот раз грани — 3 пары прямоугольников. Поэтому формула площади поверхности будет состоять из суммы трёх пар площадей прямоугольников: Sпр = 2 • (ab + bc + ac).

💁🏻‍♂ Площадь полной поверхности призмы состоит из суммы боковой поверхности и двух площадей основания. С основаниями все более менее понятно, а вот площадь боковой поверхности можно вычислить аж по двум формулам. Первая из них для прямой призмы, а вторая для наклонной призмы.

📌 У прямой призмы все грани — прямоугольники с одинаковой стороной в виде высоты. А вторая сторона каждого прямоугольника — сторона основания многоугольника в основании. Поэтому площадь боковой поверхности прямой призмы можно вычислить как произведение периметра основания на высоту.

📌 У наклонной призмы все грани — параллелограммы, поэтому базовый способ для нахождения площади поверхности — считать каждую грань по отдельности и суммировать все грани. Но это не сильно действенный способ потому, что долго и дорого так делать на экзамене, в задачах чаще всего работает другая формула.

✅ Площадь боковой поверхности наклонной призмы равна произведению бокового ребра на периметр перпендикулярного сечения этому ребру. То есть по сути это та же формула, что и для прямой призмы, только вместо периметра основания используем периметр перпендикулярного сечения, а вместо высоты используем ребро.

👉🏻 Последняя из действенных формул — площадь боковой поверхности правильной пирамиды. Площадь полной поверхности равна сумме площадей боковой поверхности и основания. Все грани правильной пирамиды – равные треугольники, у которых одинаковая высота в виде апофемы боковой грани, и равные стороны основания.

🌟 Поэтому площадь боковой поверхности равна произведению полупериметра на апофему. Одна вторая здесь возникает из-за того, что это коэффициент в каждой площади треугольника грани. 

На ЕГЭ нет подсказок в виде формул, поэтому сохраняй картинку, запоминай формулы и применяй их к задачам💕