Окружность, описанная около треугольника

Описанная около треугольника окружность — это окружность, которая проходит через все три вершины треугольника. Вокруг любого треугольника можно описать окружность, причём единственным образом. Как только мы описываем окружность вокруг треугольника возникает целых четыре отличных свойства.

✅ Во-первых, центр описанной окружности лежит на пересечении серединных перпендикуляров. (это свойство используется редко)

✅ Во-вторых, если сторона треугольника является диаметром, то треугольник прямоугольный.

✅ В-третьих, теорема синусов — отношение любой стороны треугольника к синусу противолежащего угла равно двум радиусам описанной окружности.

✅ В-четвертых, площадь треугольника можно найти через радиус описанной окружности:

S = (abc)/(4R), где a, b, c — стороны треугольника, а R — радиус описанной окружности.

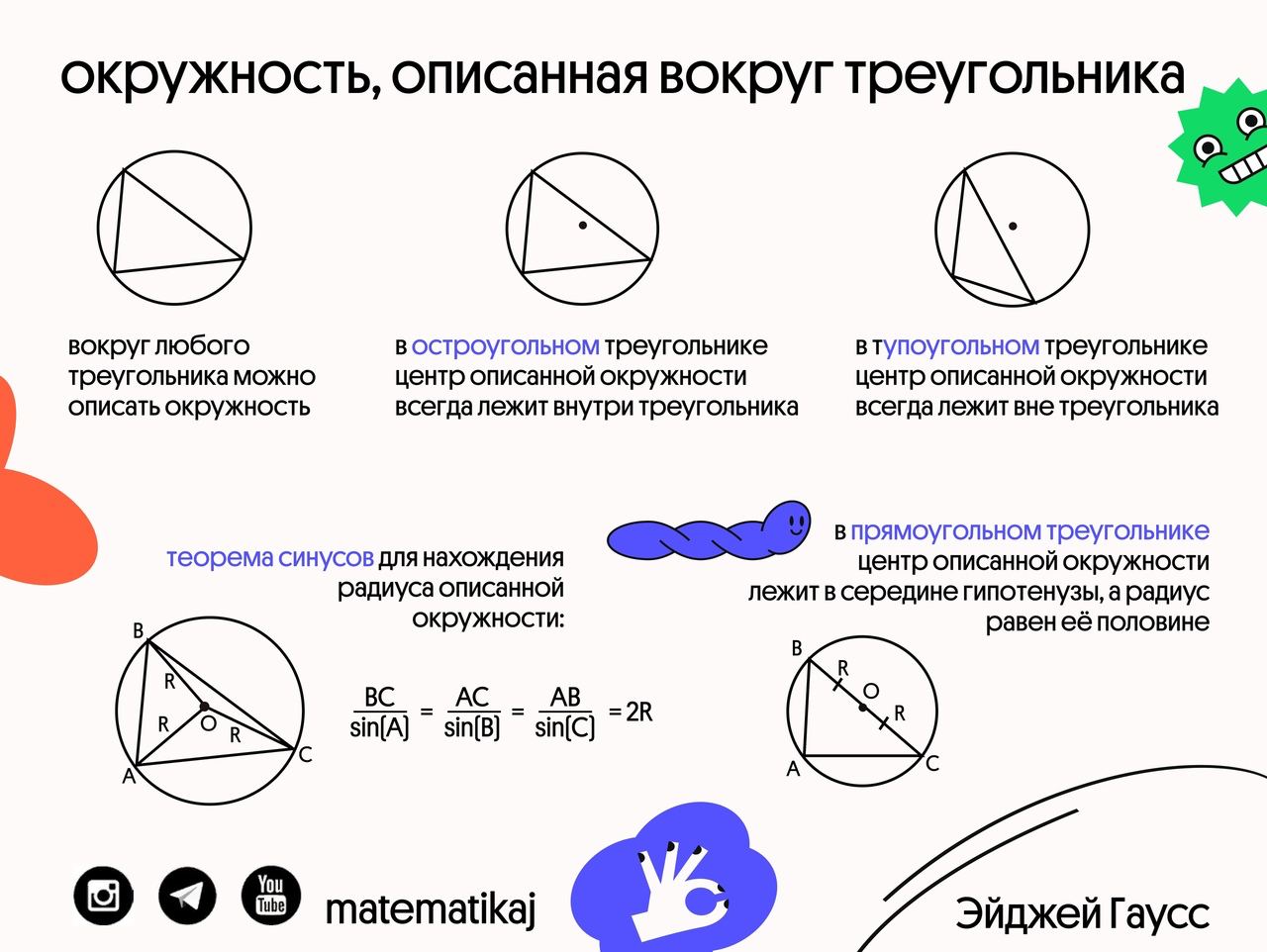
👉🏻 Все факты запечатлены на картинке, на них можно смело смотреть, запоминать и пользоваться.