Углы

Угол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки.

Стороны угла – лучи, которые образуют угол.

Вершина угла – точка, из которой выходят лучи.

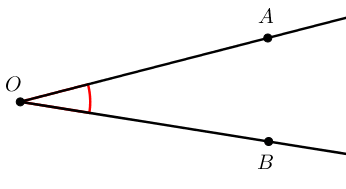
Угол называют тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные на сторонах угла.

Важно: в названии буква, обозначающая вершину угла, стоит между двумя буквами, обозначающими точки на сторонах угла. Так, угол, изображенный на рисунке, можно назвать: ∠AOB  или ∠BOA,  но ни в коем случае не ∠OAB, ∠OBA, ∠ABO, ∠BAO.

Величину угла измеряют в градусах: ∠AOB=24°.

Виды углов:

• Прямой (ровно 90 градусов)
• Острый (меньше 90 градусов)
• Тупой (больше 90 градусов и меньше 180 градусов)
• Развёрнутый (ровно 180 градусов)

1. Биссектриса угла

Биссектриса угла – это луч с началом в вершине угла, делящий его на два равных угла.

Или

Биссектриса угла – это геометрическое место точек, равноудаленных от сторон угла.

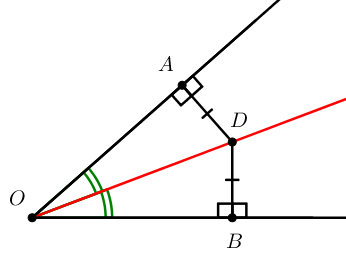
OD – биссектриса угла ∠AOB. Она делит этот угол на два равных угла.

∠AOD=∠BOD=∠AOB/2

Точка D – произвольная точка на биссектрисе. Она равноудалена от сторон OA и OB угла ∠AOB.

2. Углы, образованные при пересечении двух прямых

Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.

Свойство: вертикальные углы равны.

Смежные углы – пара углов, у которых одна сторона общая, а две другие стороны расположены на одной прямой.

Свойство: сумма смежных углов равна 180°.

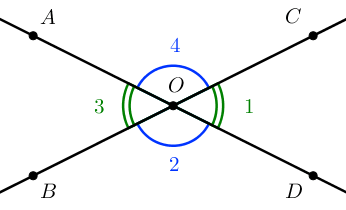
Пример

Пары углов: (1) и (3), (2) и (4) называются вертикальными.

По свойству вертикальных углов:

∠COD=∠AOB

∠BOD=∠AOC

Пары углов: (1) и (2), (2) и (3), (3) и (4), (4) и (1) называются смежными.

По свойству смежных углов:

∠COD+∠DOB=180°∠DOB+∠BOA=180°∠BOA+∠AOC=180°∠AOC+∠COD=180°

 3. Углы, образованные при пересечении двух прямых секущей

Прямая, пересекающая две заданные прямые, называется секущей этих прямых.

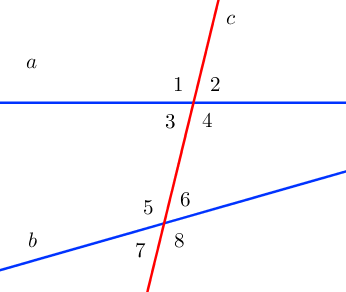
Существует пять видов углов, которые образуются при пересечении двух прямых секущей.

Пары углов: (1) и (5), (2) и (6), (3) и (7), (4) и (8) называются соответственными.

(Легко запомнить: они соответствуют друг другу, похожи друг на друга).

Пары углов: (3) и (5), (4) и (6) называются внутренними односторонними.

(Легко запомнить: лежат по одну сторону от секущей, между двумя прямыми).

Пары углов:(1) и (7), (2) и (8) называются внешними односторонними.

(Легко запомнить: лежат по одну сторону от секущей по разные стороны от двух прямых).

Пары углов:(3) и (6), (4) и (5)называются внутренними накрест лежащими.

(Легко запомнить: лежат между двумя прямыми, расположены наискосок друг относительно друга).

Пары углов: (1) и (8), (2) и (7) называются внешними накрест лежащими.

(Легко запомнить: лежат по разные стороны от двух прямых, расположены наискосок друг относительно друга).

Если прямые, которые пересекает секущая, параллельны, то углы имеют следующие свойства:

• Соответственные углы равны.
• Внутренние накрест лежащие углы равны.
• Внешние накрест лежащие углы равны.
• Сумма внутренних односторонних углов равна 180°.
• Сумма внешних односторонних углов равна 180°.

4. Сумма углов многоугольника

Сумма углов произвольного n-угольника вычисляется по формуле:

Sn=180°⋅(n−2)

где n – это количество углов в n-угольнике.

Пользуясь этой формулой, можно вычислить сумму углов для произвольного n-угольника.

Сумма углов треугольника: 

S3=180°⋅(3−2)=180°

Сумма углов четырёхугольника: 

S4=180°⋅(4−2)=360°

Сумма углов пятиугольника: 

S5=180°⋅(5−2)=540°

Так можно продолжать до бесконечности.

Правильный многоугольник – это выпуклый многоугольник, у которого все стороны равны и все углы равны.

Некоторые правильные многоугольники: 

Чтобы найти величину угла правильного n-угольника, необходимо сумму углов этого многоугольника разделить на количество углов.

αn=180°⋅(n−2)n