Производной функции y=f(x) в данной точке х0 называют предел отношения приращения функции к соответствующему приращению его аргумента при условии, что последнее стремится к нулю (очень сложное и непонятное определение…):
f’(x0)=lim(f(x0)/x) x —> 0
Дифференцированием называют операцию нахождения производной.
(f(x)±g(x))′=f′(x)±g′(x)
(f(x)·g(x))′=f′(x)·g(x)-f(x)·g(x)′/g2(x)
(f(x)/g(x))′=f′(x)·g(x)+f(x)·g(x)′
f(g(x))′=f′(g(x))·g′(x)
Если материальная точка движется прямолинейно и её координата изменяется в зависимости от времени по закону x(t), то мгновенная скорость данной точки равна производной функции. v(t)=x′(t)
Напомним, что уравнение прямой, не параллельной осям координат, можно записать в виде y=kx+b, где k – угловой коэффициент прямой. Коэффициент k равен тангенсу угла наклона между прямой и положительным направлением оси Ох.
k=tgα
Производная функции f(x) в точке х0 равна угловому коэффициенту k касательной к графику в данной точке:
f′(x0)=k
Следовательно, можем составить общее равенство:
f′(x0)=k=tgα
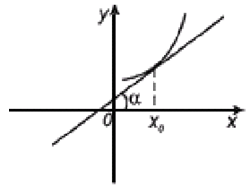
На рисунке касательная к функции f(x) возрастает, следовательно, коэффициент k>0. Так как k>0, то f′(x0)=tgα>0. Угол α между касательной и положительным направлением Ох острый.
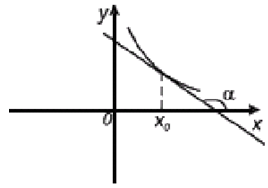
На рисунке касательная к функции f(x) убывает, следовательно, коэффициент k<0, следовательно, f′(x0)=tgα<0. Угол α между касательной и положительным направлением оси Ох тупой.
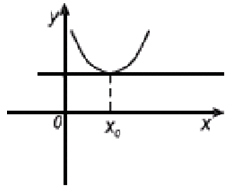
На рисунке касательная к функции f(x) параллельна оси Ох, следовательно, коэффициент k=0, следовательно, f′(x0)=tgα=0. Точка x0, в которой f′(x0)=0, называется экстремумом.
Производная так же применяется для нахождения промежутков возрастания и убывания функции:
Если f′(x)>0 на промежутке, то функция f(x) возрастает на этом промежутке.
Если f′(x)<0 на промежутке, то функция f(x) убывает на этом промежутке.
Авторизуйтесь, чтобы оставить комментарий.